The intended audience of this article is the accountant familiar with FASB / IASB guidance and present value calculations. Most of the calculations presented below will be familiar, though there may be some specifics invoked by Lucernex that are important to note.
The accompanying Core Illustration spreadsheet is editable. In particular, you are encouraged to experiment with the values in the Understanding and Using the Core Illustration section below for different scenarios and to see how the values change. Primarily, however, we left it editable so that you can examine the Excel formulas used.
Calculations in Lucernex are executed with Java code to high precision. While the mathematics are the same, there may be some slight differences between an Excel calculation and Lucernex calculation, since some of the formulas involve high powers of small numbers. It is not the intent of the Core Illustration to match Lucernex to the penny in a number-to-number calculation, but rather to inform you how Lucernex approaches the mathematics.
Download the Core Illustration document to follow along.
Understanding and Using the Core Illustration
The quantities in this section can be modified to mimic scenarios of interest to you.
Interest Rate
This is the annual IBR or discount rate in percent. For the Core Illustration we use months for periods, so the monthly interest rate is the Interest Rate/12. Annual Interest Rate here is denoted r.
Days in Month
In the Core Illustration, this is the actual number of days in a month. For example, 31 days for period 1, and 28 days for period 2. Initially we have set up the illustration with January being period 1, but you can restructure the days per period to effectively arrive at a schedule starting any month. For leap years, you can change period 2 days to 29 if desired for the one or two times this happens during your schedule. Denoted here di, where i is the period number. For example, if period 1 is January, then d1 = 31.
Lucernex also supports 4-5-4 and 4-4-5 and 13-period accounting, but that is not included in the Core Illustration.
Pay Day
Pay Day is the day of the month the rent is paid. For beginning of the month (BOP), enter 1. For end of the month (EOP), enter 31. The Core Illustration accounts for months with less than 31 days by taking the minimum of 31 and the length of the month. Denoted here Dp.
Start Day of Month
This is the day of the month that the schedule starts. This affects the first period calculations especially, since it will be a partial month. Denoted here Ds.
Cash Payments
This is the column of rent payments through the term of the lease, including likely options. In the Core Illustration, we have pre-populated an escalation in the middle of a five-year lease term. You can enter in any payment structure you want by populating this column with the rent payments over the lease term. Denoted Ci, where i is the period number in the lease.
The Single Lease Expense is denoted Cs, which is the average of the cash payments over the life of the lease:
Quick Overview: How to do a Present Value (PV) Calculation
Present value is based on the principle of “time is money” in the sense that money that is paid a month from now is less valuable than money paid today. It gets reduced by an amount that depends on the interest rate or discount rate entered into the system for the calculation.
Let’s suppose that the payment is going to be C = $10,000, and the annual discount rate is r = 5%.
For 12-period accounting—which includes fiscal calendars that are monthly, 4-4-5, or 4-5-4—the period interest rate is r/12. For 13-period accounting, the period interest rate is r/13. For the example illustrated here, we will use 12-period accounting.
The general formula is:
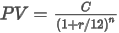
where n is the number of periods over which the reduction is taking place.
Example 1: PV’ing over one month
Here n = 1, and so PV = ($10,000) / [1+(. 05/12)]1 = $9,958. 51
Example 2: PV’ing over five months
Here n = 5, and so PV = ($10,000) / [1+(. 05/12)]5 = $9,794.25
Example 3: PV’ing over a partial month or period
Here the prescription we use is that we PV by the number of days. So suppose the payment is on April 1, and we are PV’ing back to March 15 rather than back to March 1. This is 17 days out of 31 days in March, and so n = 17/31 = 0. 548
Since n = 0. 548, PV = ($10,000) / [1+(. 05/12)]0. 548 = $9,977.23
Notice that PV’ing can be compounded so that if you want to PV by four months plus 3 days in a 30 day month, then n=4. 1, or alternatively you can PV by four periods and then PV again by the partial period.
Understanding the Calculations
Initial Period Length
This is the fraction of the first period after the Start Day of the Month to the end of the month. Denoted L0. This is calculated by the formula:
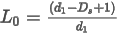
For example, if the Start Day of the Month is 1, then L0 will be 1. 00. If the Start Day of the Month is 15 in a 31-day first month, then L0 will be 0. 548 = (31 – 15 + 1)/31.
Payment Period Length
This is the fraction of the current period up to the Pay Day Dp.
Lucernex does not calculate interest on the Pay Day, and this policy affects the Period Interest Paid. This is often missed by clients in an initial comparison.
The Payment Period Length Li is calculated by the formula:
For example, if you are calculating a beginning-of-period (BOP) schedule, Li will always equal zero. If the Pay Day is the 16th of the month, then in a 30-day month, Li will equal 0. 5. If you are calculating an end-of-period (EOP) schedule, then Li will be 30/31 for a 31-day month and 27/28 for a 28-day month. Li is never the length of the whole month, even for an EOP schedule.
Period Present Value (PV)
This is the Cash Payment, discounted to present value (PV) from the period the payment will be made. This is a standard present-value calculation. Denoted as PVi, the period PV is calculated by the formula:
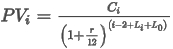
The power in this expression is worth looking at, as it is sometimes represented as just the period number i or i-1. In Lucernex, we count only the present period up to the Pay Day and only the initial period after the Start Day of the Month. This method gives a more detailed present-value calculation including the partial months between the start of the schedule and the current Pay Day. However, if you are doing BOP accounting and the schedule starts on the first day of the month, this power will in fact be i-1.
Also, note that the power in the Period PV calculation for the first period is calculated differently to account for the partial month if the Start Day Ds is not 1.
Initial Liability Balance
This is the total of all of the Period Payment Present Values over the life of the lease.
Period Net Present Value (NPV) of Future Payments
This is the present value of the sum of all future Period PVs, from the end of the lease, denoted NPVi. It is a straightforward present-value calculation, given by
where n is the number of terms in the lease.
Period Interest Paid
This is the interest that contributes to the current liability balance, and it is composed of two values:
-
The interest paid on the period Cash Payment up to the Pay Day, and
-
The interest paid on the Period Net Present Value of Future Payments.
The Period Interest Paid is denoted here PIi and is given by:
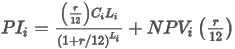
Notice that the first value in the sum—interest on the current cash payment—is prorated by the Period Payment Length and then adjusted to present value at the beginning of the period. This first value is calculated a little differently for the first schedule term, to reflect the Initial Period Length, allowing for the case where the Start Day of the Month for the schedule is not on the 1st.
Following the Schedule
The Liability Balance and the Asset Balance now are calculated based on the numbers described in the previous section. These are calculated differently for Finance leases and Operating leases. In the Core Illustration, the Initial Liability Balance and the Initial Asset Balance are the same.
Finance Leases
-
The Liability Balance for period i is calculated by taking the Liability Balance for the previous period i-1, subtracting the Cash Payment, and adding the Period Interest Paid:
-
The Asset Balance for period i is calculated by taking the Asset Balance for the previous period i-1, subtracting the Initial Liability Balance divided by the number of periods n:
-
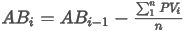
In a Finance lease, the Asset Amortization Expense—the amount the asset balance decreases from month to month—is constant for each period.
Operating Leases
-
The Liability Balance for period i is calculated by taking the Liability Balance for the previous period i-1, subtracting the Cash Payment, and adding the Period Interest Paid:
-
The Asset Balance for period i is calculated by taking the Asset Balance for the previous period i-1, subtracting the Straight-lined Cash, and adding the Period Interest Paid:
Comparing the Core Illustration to Lucernex Schedules
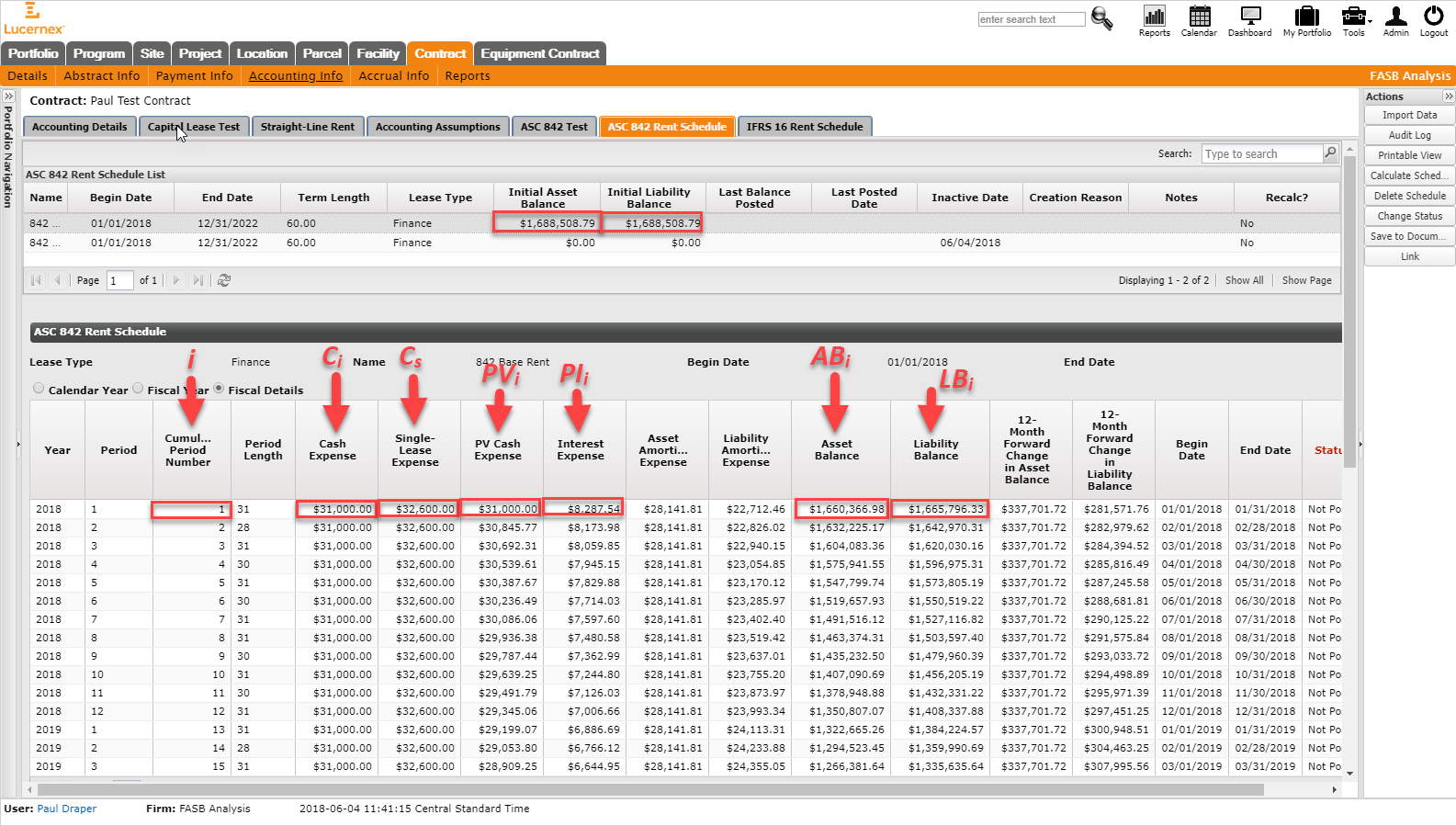
In this section, we show where the numbers above appear in the ASC 842 / IFRS 16 accounting schedules as shown in Lucernex.
The Core Illustration is built as a five-year lease with initial monthly rent payments of $31,000, and escalations of an additional $2,000 at two year intervals. Therefore, the rent payments are $35,000 for the last year. The discount rate is set at 6% initially. For the purpose of comparison, this scenario has the Pay Day as the first of the month and the Start Day of the Month is also the first of the month. Also for the purpose of the comparison here, we’re showing the case of a Finance lease.
We performed the following actions in Lucernex:
-
Created a lease with the rent payment structure specified above,
-
Added basic accounting assumptions for the term of the lease,
-
Assigned a 6% discount rate, and
-
Created an ASC 842 Finance lease accounting schedule.
The result is shown in the following screen capture, where we have called out the columns with the symbolic labels of the quantities above. The numbers in the Lucernex schedule correspond to the numbers in the Core Illustration spreadsheet, with small variations due to a slight difference in the calculation engines.
The following variables correspond to these columns:
-
i: Cumulative Period Number column
-
Ci: Cash Expense column
-
Cs: Single Lease Expense column
-
PVi: PV Cash Expense column
-
PIi: Interest Expense column
-
ABi: Asset Balance column
-
LBi: Liability Balance column
The Initial Asset Balance and Initial Liability Balance are shown in the boxes at the top. For reference, we have marked period 1 numbers so that you can see the comparative numbers in the Core Illustration.
A few other numbers in the Lucernex schedule are worth explaining:
-
Asset Amortization Expense: Amount the Asset Balance is decremented in that period.
-
Liability Amortization Expense: Amount the Liability Balance is decremented in that period.
-
12-Month Forward Change in Asset Balance: Sum of the Asset Amortization Expenses for the next 12 periods.
-
12-Month Forward Change in Liability Balance: Sum of the Liability Amortization Expenses for the next 12 periods.
For completeness, we show here the end of the accounting schedule, so that you can see how the Core Illustration results mimic those shown in Lucernex, as well.
Try variations of the parameters in the Understanding and Using the Core Illustration section above in the Core Illustration to see their effect on the calculations. We also encourage you to set up a similar lease in Lucernex and run a schedule as an Operating lease to see how the Core Illustration lines up to that case as well.
Finally, please remember that this Core Illustration document is intended to provide insight into Lucernex calculations using some basic scenarios. Lucernex can handle a much wider set of scenarios that will have impact on accounting schedules, and those scenarios are not reflected in this Core Illustration at this time.
